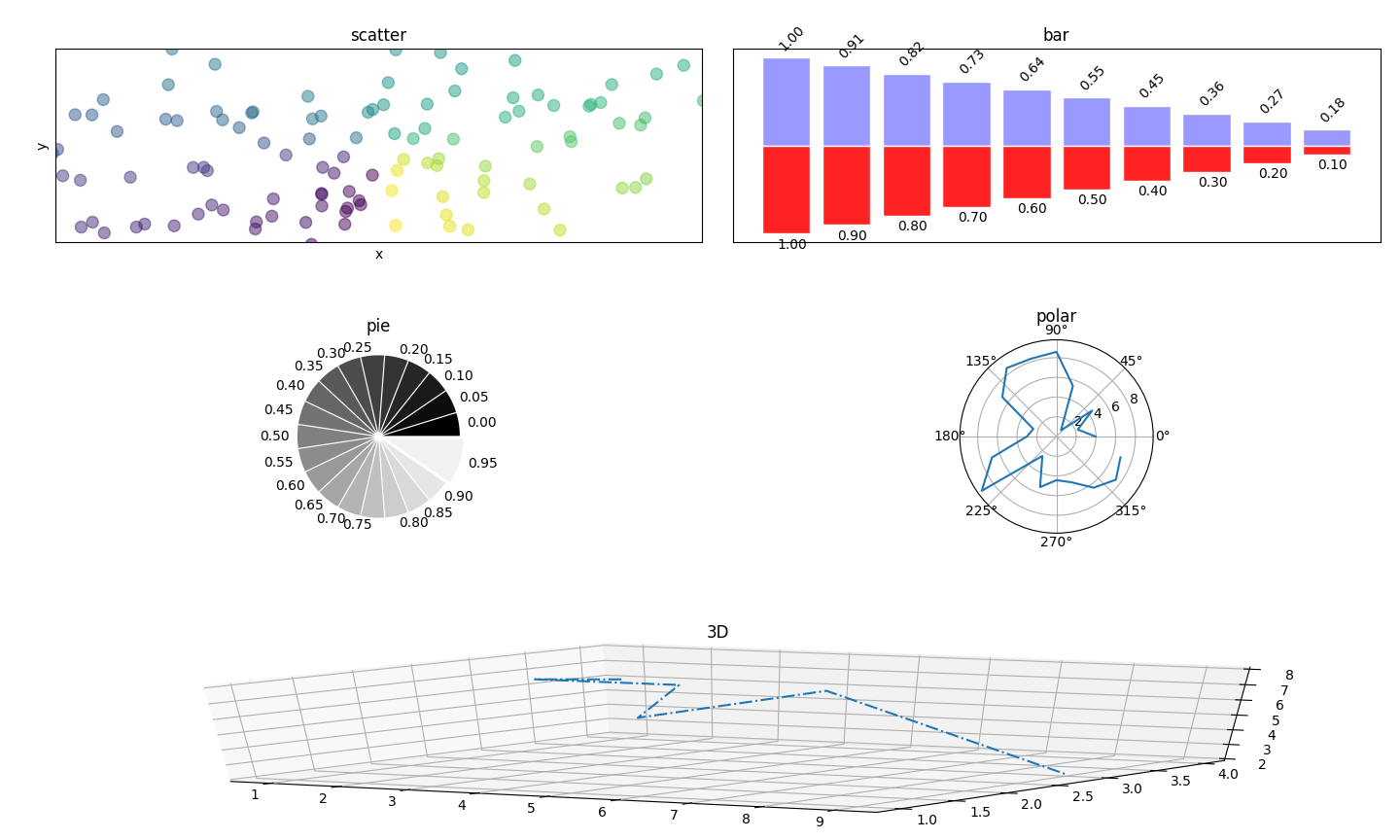
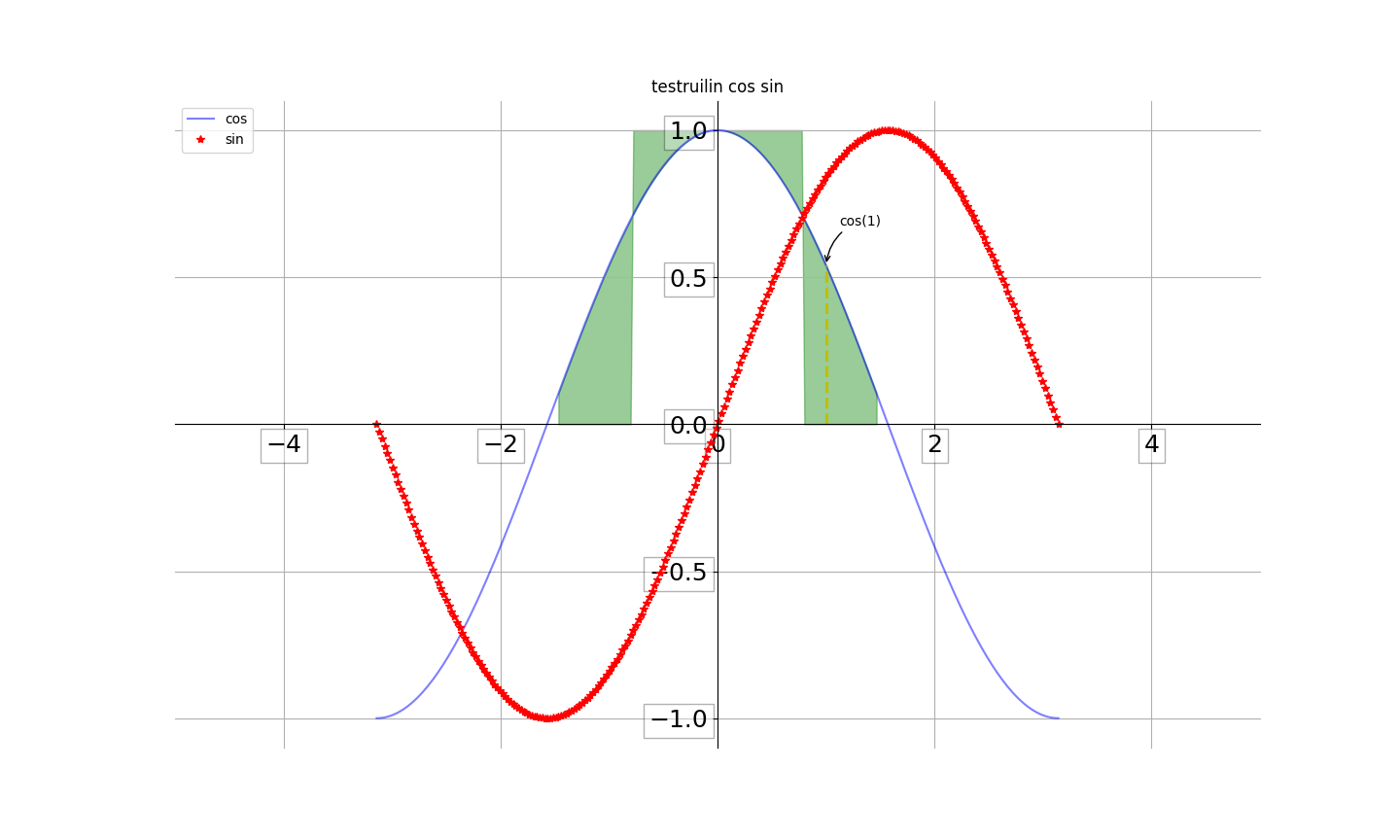
xlrd基本操作并配合matplotlib绘图笔记
一个简单的小例子快速了解如何利用xlrd读取excel并借助plt绘图
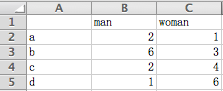
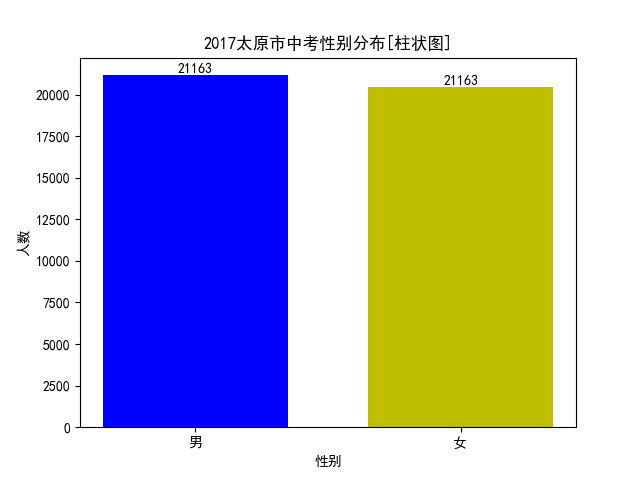
//之前代码有误,导致上图显示女生数量与男生一样,代码已改正
#encoding=utf-8
import xlrd
import matplotlib.pylab as plt
from pylab import *
def main():
book=xlrd.open_workbook('./pdtest.xlsx')
sheet_name = book.sheet_names()[0]#获得指定索引的sheet名字
print sheet_name
sheet=book.sheet_by_name('sheet1')
rows=sheet.nrows#行数
cols=sheet.ncols#列数
print rows,cols
row_data=sheet.row_values(0)
col_data=sheet.col_values(0)
print row_data,col_data
cell=sheet.cell_value(1,2)
print cell
for i in range(rows):#每行数据
print sheet.row_values(i)
col1=sheet.col_values(1)[1:]#去掉列名称 打印指定列
print col1
k = 0
for i in col1:
print int(i)
if int(i)==int('2'):
k+=1
print k
book1=xlrd.open_workbook('./reg.xls')
#sheet_name1=book1.sheet_names()[0]
#print sheet_name1
list=book1.sheets()[0]
nrows=list.nrows
print nrows
print "------------------"
col2=list.col_values(4)[1:]
g = 0
b = 0
for i in col2:
if i == u"\u5973":
g=g+1
if i == u"\u7537":
b+=1
print g,b
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(1)
plt.bar(left=0,height=b,width=0.35,align="center",color="b",label="boy")
plt.bar(left=0.5,height=g,width=0.35,align="center",color="y",label="girl")
plt.title(u"2017太原市中考性别分布[柱状图]")
plt.xlabel(u"性别")
plt.ylabel(u"人数")
plt.xticks((0, 0.5), (u"男", u"女"))
plt.text(0, b+0.05, "%d" % b, ha="center", va="bottom")
plt.text(0.5, g+0.05, "%d" % g, ha="center", va="bottom")
#图中有误,之前把代码里面的参数g写成了b
#plt.legend(loc="upper left")
plt.show()
if __name__ == '__main__':
main()
output:
sheet1 5 3 [u'', u'man', u'woman'] [u'', u'a', u'b', u'c', u'd'] 1.0 [u'', u'man', u'woman'] [u'a', 2.0, 1.0] [u'b', 6.0, 3.0] [u'c', 2.0, 4.0] [u'd', 1.0, 6.0] [2.0, 6.0, 2.0, 1.0] 2 6 2 1 2 41609 ------------------ 20445 21163